السلام عليكم. اليوم ننهي حديثنا عن طرق وأساليب التعرف على المصفوفات. شاهدنا في الجزئين الأول والثاني بعض الأنساق التي تميز العمليات المختلفة التي قد تقوم بها مصفوفة ما، كالإزاحة والدوران والتحجيم. وقد بقي لنا نسقان آخران يهمنا الاطلاع عليهما، ويندرجان تحت بند مصفوفات الإسقاط. ما هي مصفوفة الإسقاط؟ وكيف يكون شكلها؟ هذا ما سنجيب عنه اليوم باذن الله.
عندما نبني المجسمات فإننا نبنيها من مثلثات مكونة من رؤوس ذات إحداثيات ثلاثية الأبعاد. وعندما نريد إظهار هذه المجسمات على الشاشة المسطحة فإننا نضطر لمعرفة موقع كل مثلث على الشاشة. إذن هناك حسبة معينة تقوم بتحويل الإحداثيات الفراغية إلى إحداثيات مسطحة كي نستطيع رؤية هذه المجسمات على الشاشة. هذه العملية هي ما يدعى بالإسقاط. أي أنك تقوم بإسقاط الإحداثيات الفراغية على سطح الشاشة.
هناك طرق عدة للإسقاط، سنأخذ منها الإسقاط المتوازي (الأكسونومتري) والإسقاط الفراري (المنظوري). يُستعمل الإسقاط المتوازي بكثرة في المخططات الهندسية المعمارية والميكانيكية، فالخطوط المتوازية في الإسقاط المتوازي تحافظ على توازيها حتى بعد أن يتم إسقاطها.
كمثال، انظر معي الصورة الآتية:
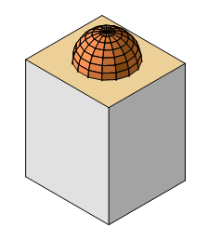
بالمقابل، في الإسقاط الفراري لا يشترط أن تحافظ الخطوط على توازيها بعد الإسقاط:
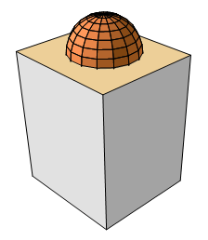
عموماً تكون مصفوفة الإسقاط هي المصفوفة الأخيرة التي تمرّ عليها رؤوس المثلثات ضمن سلسلة المصفوفات الأخرى التي يحددها المبرمج، وذلك لأننا وبعد أن نقوم بكافة عمليات الإزاحة والتدوير والتحجيم، فإننا نرغب برؤية المجسم على الشاشة، وبالتالي لا بد من إسقاط إحداثياته على سطحها.
حسناً، لننظر الآن إلى مصفوفتي الإسقاط المتوازي والفراري لنتعرف على شكليهما:
| 0 |
0 |
0 |
0.050 |
| 0 |
0 |
0.067 |
0 |
| 0 |
0.010 |
0 |
0 |
| 1 |
0.001- |
0 |
0 |
(إسقاط متوازي)
|
| 0 |
0 |
0 |
0.005 |
| 0 |
0 |
0.007 |
0 |
| 1 |
1.001 |
0 |
0 |
| 0 |
0.1- |
0 |
0 |
(إسقاط فراري) |
وهذا هو الكود لتوليد هاتين المصفوفتين:
D3DXMATRIX matOrtho,matPerspective;
D3DXMatrixOrthoLH(&matOrtho,40.0f,30.0f,0.1f,100.0f); // مصفوفة إسقاط متوازي بنافذة بأبعاد 30×40
D3DXMatrixPerspectiveLH(&matPerspective,40.0f,30.0f,0.1f,100.0f); // مصفوفة إسقاط فراري بنفس القيم أعلاه
في حالة مصفوفة الإسقاط المتوازي فإنه يصعب تفريقها عن مصفوفة مكونة من تحجيم وإزاحة. لكن بالنسبة لمصفوفة الإسقاط الفراري فإننا نلاحظ (ولأول مرة) أن العمود الأخير قد اختلف. فقد اعتدنا أن نجد الرقم 1 في الخلية السفلى من هذا العمود. أما الآن فهو في الخلية الثالثة من الأعلى، ولذلك قصة طويلة سنتفادى ذكرها اليوم. بقية العناصر تتشابه مع مصفوفة الإسقاط المتوازي.
هناك أنواع أخرى من المصفوفات لم نذكرها في سلسلة التدوينات هذه. مثلاً، مصفوفة الرؤية (view matrix) والتي من خلالها نستطيع أن نرى المشهد الفراغي من أي زاوية نظر ومن أي مسافة نشاء. هذه مصفوفة رؤية:
|
0
|
0.424-
|
0.424-
|
0.8
|
|
0
|
0.707-
|
0.707
|
0
|
|
0
|
0.566
|
0.566
|
0.6
|
|
1
|
7.071
|
0
|
0
|
تم بناء هذه المصفوفة بالكود التالي:
D3DXMATRIX matView;
D3DXVECTOR3 vec3Eye(3,5,-4); // موقع عين الناظر
D3DXVECTOR3 vec3At(0,0,0); // موقع هدف النظر
D3DXVECTOR3 vec3Up(0,1,0); // ناظم رأس الناظر
D3DXMatrixLookAtLH(&matView,&vec3Eye,&vec3At,&vec3Up);
أيضاً لا يوجد نسق معين واضح هنا، فهناك عملية دوران وإزاحة في المصفوفة (الزاوية 3×3 العليا اليسرى مليئة بالأرقام غير الصفر والواحد). في الواقع هذا هو كل ما تفعله مصفوفة الرؤية. فهي تقوم بتدوير المشهد وإزاحته لنراه من الزاوية والنقطة التي نريدها.
في أوبن جي إل يتم تحديد مصفوفة الرؤية مقرونة بمصفوفة التحويل من الفضاء المحلي إلى العالم، وتدعى هذه المصفوفة المركبة بـ ModelView. بينما في دايركت ثري دي 9 يتم تحديد كلاً من المصفوفتين بشكل مستقل (إلا أنك تستطيع أيضاً اعتماد نفس طريقة أوبن جي إل إن أردت ذلك).
بهذا أنهي حديثي عن أحد الجوانب الممتعة في المصفوفات في الرسوميات الفراغية. هناك جوانب ممتعة أخرى في المصفوفات قد أتطرق إليها إن أحياني الله لحينها، كبناء التحويلات بين أنظمة الإحداثيات بشكل يدوي، والمقلوب والمعكوس، واستخراج الدورانات. لكن تلك تدوينات أخرى…
والآن أترككم برعاية الله.