تستكمل لنا هذه التدوينة ما بدأته سابقتها في الحديث عن تطبيق مفهوم المتجهات في النظرية الموسيقية. في الحقيقة كان يفترض من هذه التدوينة أن تقدم لنا العمليات الرياضية وتأثيرها على المتجهات الموسيقية، ولكن بسبب اعتماد تعريف العمليات الرياضية على ما سأقدمه هنا آثرت تأجيلها لجزء لاحق إن شاء الله.
في هذه التدوينة سأقوم بوصف ما يسمى الفضاء الموسيقي (Music Space) أو اختصاراً (M-Space) الذي تنتمي له هذه المتجهات. حقيقةً، مفهوم الفضاء الموسيقي غير مطروح في النظرية الموسيقية الأساسية التي عمل بها ألن فورت (Allen Forte) وإنما قمت بتقديمه أول مرة وعرضه هنا لأهميته في تبرير تصرف المتجهات الموسيقية في فضائها عند تطبيق العمليات الرياضية عليها.
إذن ماهو هذا الفضاء وماهي خصائصه؟
كتعريف مختصر…
الفضاء الموسيقي هو فضاء مجرد1 مؤلف من عدد من الأبعاد2 ذات طوبولجية دورانية3.
طبعاً قد يكون التعريف السابق مبهم في بداية الأمر، ولكن بعد تبسيطه وتحليل مكوناته ستتوضح صورته بإذن الله.
المكون الأول من هذا التعريف يوصف لنا هذا الفضاء بكونه فضاء خيالي ومجرد، أي لا يوجد له تمثيل واقعي كما في حالة الفضاء الذي نعيشه والذي يمكن أن يمثل بفضاء متعامد ثلاثي الأبعاد. لذلك لا يمكن وضع تخيل بصري عام لهذا الفضاء وأقصى ما يمكن تمثيله بصرياً هو بعض الحالات الخاصة والبسيطة والتي سنمر عليها بعد قليل.
المكون الثاني من هذا التعريف هو عدد الأبعاد التي يتألف منها الفراغ الموسيقي. فعلياً لا يوجد هناك عدد محدد لهذه الأبعاد، وإنما عددها يتعلق مباشرة ببعد المتجهات الموسيقية التي تنتمي له. فعلى سبيل المثال المتجهات الموسيقية الثنائية أو الديادس (Dyads) كما تسمى موسيقياً بحاجة لفضاء ثنائي الأبعاد لاحتوائها، بينما الكوردات الثلاثية (Trichords) تتطلب فضاء بثلاثة أبعاد وهكذا بالنسبة للمتجهات ذات الأبعاد الأعلى مثل (Tetrachords, Pentachords, Hexachords) التي تحتاج لفضاءات ذات أبعاد رباعية وخماسية وسداسية على الترتيب. كما هو واضح من هذا الجزء من التعريف، من الصعب تخيل أو تمثيل فضاء بخمسة أبعاد مثلاً لذلك يبقى هذا الفضاء مجرد وتخيلي كما مر معنا في الجزء الأول من التعريف.
الجزء الأخير من التعريف هو في الحقيقة الجزء الأصعب والأهم لتأثيره مباشرة على تصرف العمليات الرياضية التي سيتم تعريفها فيما بعد. يحاول هذا الجزء من التعريف وصف ما يسمى طوبولوجية الفضاء (Space Topology) من خلال مكوناته الأساسية وهي الأبعاد. ولكن ماهو المقصود بطوبولوجية الفضاء؟ وكيف تؤثر هذه الطوبولوجية على الشكل العام للفضاء المدروس والمكونات التي تنتمي له؟
حقيقة الأمر، الإجابة عن هذه الأسئلة هي جزء أساسي وهام من أحد أفرع الرياضيات الحديثة المسماة بعلم الطوبولوجي التي قد يكون من الصعب جداً إعطائها حقها بالشرح ضمن تدوينة بسيطة. لذلك سنتكفي هنا باقتباس بعض الأفكار الأساسية من هذا العلم للتعرف عليها وعلى تطبيقاتها في حالتنا التي تتعلق بالموسيقى. بشكل عام يهتم هذا العلم بدراسة سلوك الفضاء وخصائصه مثل الاستمرارية (Continuity) والترابط بين أجزائه المختلفة (Connectivity) وغيرها من الخصائص. لتوضيح بعض هذه المفاهيم والفرق بينها سنأخذ الأمثلة البسيطة التالية.
إذا درسنا التمثيل الفراغي لفضاء الغرفة التي نعيش ضمنها الآن. سنجد أن هذا التمثيل يعتمد على ثلاثة محاور متعامدة تمتد بشكل مستمر من مركز الإحداثيات في أحد أطر��ف الغرفة وتنتهي فعاليتها بنهاية الغرفة. أي فعلياً كل من هذه الأبعاد يمكن التعبير عنه رياضياً بمجال مغلق من القيم المستمرة الذي ينتمي لفضاء الأعداد الحقيقية R1. فعلى سبيل المثال إذا كان طول الغرفة على المحور X هو 12m، عندها يمكن أن يكون التمثيل الرياضي لفضاء الغرفة بالنسبة لهذا البعد هو [0,12].
الآن وبناءً على هذا التمثيل الرياضي، ماهي الخصائص الطوبولوجية له؟
نلاحظ أن جميع أبعاد هذا الفضاء تحقق خاصية الاستمرارية على المجال المعرفة ضمنه، لأننا فعلياً نستطيع التعامل مع أية قيمة ضمن حدود هذا المجال. حسناً ولكن ماذا عن حدود المجال نفسه؟ نلاحظ هنا أن أطراف المجال لا تحقق خاصية الترابط، وذلك بسبب عدم إمكانية الانتقال من أحد أطراف المجال للطرف الآخر بشكل مباشر دون انقطاع. وهذا ما نلمسه على أرض الواقع، فلا أحد يستطيع فعلياً الانتقال آنياً من بداية الغرفة إلى نهايتها إلا إذا كان يستخدم إحدى آلات الانتقال الآني التي تعج بها أفلام الخيال العلمي أو كان على علم بأحد الثقوب الدودية (Wormholes) التي يفترض العلماء وجودها في بعض الأماكن من الفضاء. إذن أين يمكن أن نجد فضاء يحقق خاصية الترابط بين أطراف المجال؟
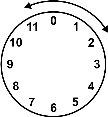
في الحقيقة هناك الكثير من الحالات التي تمثل بفضاء ذو أطراف مترابطة. على سبيل المثال، إذا أخذنا الزمن كبعد إضافي للفضاء الذي نعيش فيه ودرسنا تمثيله السائد على الساعة ذات العقارب، سنلاحظ في هذا التمثيل أن مجال الساعات هو في الحقيقة مجال مستمر بين [0,12) ولكنه في نفس الوقت مترابط أيضاً بين أطراف هذا المجال. السبب في هذا الترابط هو أنه من الممكن لعقرب الساعة الانتقال من نهاية المجال عند الساعة 11:59 إلى بدايته عند الساعة 0 مرة أخرى بشكل مباشر ودون انقطاع.

هذه الحقيقة البسيطة يمكن تعميمها لأي بعد دائري. على سبيل المثال حدود مجال زوايا الدائرة التي تتمثل بالمجال [0,2π) أيضاً تعتبر مجال مترابط لأن الزاوية 2π على طرف المجال تؤدي للوصول للزواية 0 على الطرف الآخر من المجال مباشرة.
في علم الطوبولوجي يُمثل البعد الذي يحقق خاصية الترابط على حدود مجاله بدائرة S1
الآن وبعد كل هذا النقاش ما هي الخصائص الطوبولجية للفضاء الموسيقي الذي يهمنا بالأساس؟
في حقيقة الأمر تحقق أبعاد الفضاء الموسيقي خاصية ترابط حدود المجال التي ذكرناها لذلك طوبولوجياً يمكن تمثيلها بالدائرة S1. وأقرب مثال يمكن استخدامه لتخيل شكل البعد الموسيقي هو مثال الساعة ذات العقارب. فإذا افترضنا أن أدلة النغمات التي ذكرناها سابقاً من 0 إلى 11 مصطفة على محيط دائرة بشكل مشابه لما نراه في الساعة ذات العقرب نكون قد وصلنا لتوصيف بسيط وكافي لبعد من الفضاء الموسيقي. بناءً على هذا الوصف، يكون الفرق بين العلامة الموسيقية ذات الدليل 2 والعلامة ذات الدليل 11 ليس 9 كما هو متوقع في الفضاءات التي لا تحقق خاصية الترابط، وإنما الفرق هو 3 لأنه وبسبب ارتباط أطراف المجال يمكننا الانتقال من الدليل 11 للدليل 2 من خلال ثلاث خطوات كالتالي: 11->0->1->2.
إلى هنا نكون قد تمكنا من توصيف طبيعة أبعاد الفضاء الموسيقي بناء على بعض المفاهيم الأساسية في الرياضيات، ولكن للأسف هذا لا يكفي، لأن الفضاء المدروس هو تركيب من عدد من الأبعاد وليس مؤلف من بعد وحيد. لذلك نحن بحاجة لاستنتاج الخصائص الطوبولوجية العامة للفضاء بناءً على خصائص أبعاده المستقلة. لتبسيط المسألة سنأخذ فضاء موسيقي مؤلف من بعدين ونرى ما هو شكل هذا الفضاء بعد أن علمنا أن أبعاده تمثل فضاء طوبولوجي دائري S1. علم الطوبولوجي يقدم لنا الحل لمثل هذا المسألة من خلال مسطح فراغي يحقق خصائص الارتباط والاستمرارية في كلا البعدين. هذا المسطح الناتج هو عبارة عن حلقة فراغية (Torus) يرمز له في علم الطوبولوجي بالفضاء T2.
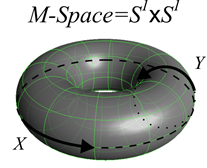
هذا هو فعلياً الشكل الحقيقي للفضاء الموسيقي المؤلف من بعدين (X,Y) فقط، حيث على سطح هذا الفضاء الملتوي تقع جميع الكوردات الموسيقية الثنائية بتوضعها الفراغي الصحيح الذي تحققه الخصائص الطوبولوجية للفضاء.
من الواضح أن هذا التمثيل الذي قدمته هنا قد لا يكون مألوفاً للكثير وذلك بسبب أبعاده الدائرية، ولكن في حقيقة الأمر لا يهمنا كثيراً تمثيل الفضاء بصرياً لأنه وبكل الأحوال من غير الممكن تمثيل أي فضاء موسيقي أكبر من بعدين. ما يهمنا معرفته من الناحية النظرية هو أن أي فضاء موسيقي يمكن تشكيله من خلال عملية ضرب كارتيسية لأبعاده الدائرية، ففي حال فضاء موسيقي بثلاثة أبعاد يكون التعبير الرياضي له هو: S1×S1×S1=T3 أي أن الفضاء الناتج هو عبارة عن الحلقة T3. بنفس الطريقة يتم التعبير عن أي فضاء موسيقي بأي بعد كان.
أعتقد أننا أدرنا اليوم رؤوسنا بما يكفي مع كل هذه الفضاءات الدورانية والطوبولوجيات الملتوية. سأتوقف هنا بعد أن أخذنا فكرة بسيطة حول ماهية الفضاء الموسيقي الذي سنستخدمه كأساس عام لتعريف جميع العمليات الرياضية وتبرير تصرفها موسيقياً.
إلى ذلك الوقت أترككم في رعاية الله...