المقدمة
أحد أهم العناصر التي تشكّل ألعاب الفيديو ثلاثية الأبعاد اليوم هي الشخصيات وحركتها، حيث إن معظم الألعاب التجارية تستخدم الشخصيات بطريقة أو بأخرى، ولا أتحدث هنا عن الشخصيات البشرية فقط، كلا بالتأكيد، هنالك الحيوانات والوحوش، الشخصيات الكارتونية، وكذلك الرجال الآليين وغير ذلك، كل ذلك يصنف من ضمن الشخصيات، وكل ذلك يستخدم الأسس والمفاهيم ذاتها التي سأتكلم عنها في هذه المقالة.
لنقابل فنسنت، وهو إنسان تجارب (التطور الطبيعي لفئران وقرود التجارب) أعارتنا إياه إحدى الجهات السرية التي لن يتم الإفصاح عنها للأسباب المعرفة...
سرّي للغاية:
- فنسنت / إنسان تجارب
- يحب أن يلبس البدلات السوداء
- يحب أن يضع نظارات سوداء
- يستجيب للأوامر بدون مساءلة أو تردد
- يرجى إطعامه مرتين يومياً وعدم كشف سره لأي شخص غير مرخص.

هل هذه المقالة مناسبة لي؟
كتبت هذه المقالة لتستهدف مستوى يقع بين المتوسط والمتقدم، لذلك فإني أفترض إنك تجيد لغة ++C ولديك معلومات جيدة عن تقنيات وأساليب الرسوميات الفورية (على سبيل المثال لا الحصر/ تعرف معنى كلمة vertex في عالم الرسوميات الفورية)، كذلك من المفيد أن تستطيع التعامل مع أو فهم الكود الذي يستخدم Direct3D9 لأن جميع الأمثلة في المقالة تستخدمه للإظهار.
إذا لم تكن تجيد لغة ++C فسأطلب منك أن تتراجع خطوة، وتبحث عن كتب ودروس تغطي البرمجة بلغة ++C (وهنالك الكثير). أما إن لم تكن تملك الكثير من المعلومات عن الرسوميات الفورية فأنصحك بدراسة إحدى واجهات البرمجة الفورية (DirectX أو OpenGL) أو دراسة إحدى محركات الرسوميات المتوفرة من أمثال Ogre3D.
هل هذه المقالة نظرية؟ أو هل ستملأ رأسي بالكلام الفارغ فقط؟
لك كل الحق في أن تسأل! هذه المقالة تتألف من جزئين، الأول يشرح المفاهيم التي تستند عليها حركة الشخصيات عموماً، أما الجزء الثاني فسيدرس بشكل تطبيقي مكتبة مختارة لتحريك الشخصيات.
ضمن الجزء الأول، سأقدم عدداً من التطبيقات والأمثلة الصغيرة التي ستطبّق ما نناقشه من كلام نظري قدر الإمكان. أما في الجزء الثاني، فسنتعلم استخدام المكتبة المختارة لنصنع مشروعاً كاملاً في نهاية المطاف، وبالطبع "نستغل" فيه وجود فنسنت (ضحكة شريرة).
حول الملفات والمشاريع المرفقة مع هذه المقالة
تم جمع الملفات والمشاريع المرفقة لكل جزء في ملف مضغوط واحد، المشاريع المرفقة مع الجزء الأول تتضمن:
- تطبيق البنية الشجرية (Hierarchy)
- تطبيق الجلد (Skin)
- تطبيق الحركة التحوّلية (Morphing)
جميع المشاريع تم عملها باستخدام Visual C++ 2008 Express وهي تستخدم Direct3D9، سوف تحتاج طقم تطوير DirectX9 (إصدارة June 2007 على الأقل) لتستطيع بناء البرامج من الكود بشكل صحيح. الملف winmain.cpp هو أهم جزء من التطبيق وهو ما يجب أن تبدأ به.
الكود تم التعليق عليه باللغة العربية قدر الإمكان، ومن ضمن ذلك كود المظللات (Shaders) المستخدمة.
أما الملفات المرفقة فهي كالآتي:
•مصدّر المجسّمات المستخدم في تطبيق الحركة التحوّلية
•فيديو الحركة الديناميكية من NaturalMotion
المشاريع المرفقة مع الجزء الثاني هي كالتالي:
- تطبيق تحميل وتحريك فنسنت (FFP)
- تطبيق تحميل وتحريك فنسنت (PP)
- تطبيق التخرّج
بالنسبة لمشاريع الجزء الثاني، إذا كنت تود بناء التطبيقات من المصدر بنفسك، يجب أن تضيف مسار مكتبة Cal3D إلى قائمة المسارات في بيئة التطوير الخاصة بك.
أما الملفات المرفقة فهي:
- الشفرة المصدرية الكاملة لمكتبة Cal3D بالإضافة إلى الأمثلة والمصدّرات والأدوات.
- مكتبة Cal3D (يمكنك استخدامها مباشرة) مبنية مسبقاً مع تطبيقات عرض الشخصيات المرفقة.
- مصدّرات للبرامج التالية: 3D Studio MAX 2.5/3/4/5/6/7/8, Maya 5/6, Blender, MilkShape.
- وثائق الشفرة المصدرية الكاملة للمكتبة بصيغة HTML مبنية باستخدام Doxygen.
- شخصيتين بحركة كاملة بصيغة Cal3D يمكنك استخدامهما للتجربة.
الجزء الأول: أسس ومفاهيم حركة الشخصيات في التطبيقات الفورية
سنناقش خلال هذا الجزء ثمانية مفاهيم أساسية تستند عليها حركة الشخصيات، كل مفهوم يعتمد على المفاهيم التي سبقته لذلك فأنا أنصح بقراءة المفاهيم حسب التسلسل الموجود.
المفاهيم التي سيتم مناقشتها هي كالآتي:
- البنية الشجرية (Hierarchy)
- الحركة العظمية (Skeletal Animation)
- الجلد (Skin)
- الوضع الأساسي (Initial Pose)
- مفاتيح الحركة (Animation Keyframes)
- مزج الحركة (Animation Blending)
- حركة الوجه (Facial Animation)
- حركة الملابس (Cloth Simulation)
- الحركية الأمامية (Forward Kinematics) والحركية العكسية (Inverse Kinematics)
والآن.... ليبدأ المرح!
المفهوم الأول: البنية الشجرية (Hierarchy)
انظر إلى إحدى ذراعي فنسنت الآن (الشكل 1)، تتألف الذراع من: العضد، الساعد، ثم اليد. تربط بين هذه الأجزاء علاقة حركية محددة:
- يمكن أن تتحرك اليد بطريقة مستقلة، أي لن يتأثر الساعد والعضد بتلك الحركة.
- عندما يتحرك الساعد، سوف تتحرك اليد معه، ولكن العضد لن يتأثر.
- عندما يتحرك العضد، فسيحرك معه الساعد، والساعد بدوره سيحرك اليد.
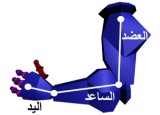
توصف هذه العلاقة بأنها تتخذ بنية شجرية، لأنها تبدأ من العضد وتمتد حتى اليد وكل جزء يؤثر على الأجزاء التي تقع بعده بحيث تشبه بذلك فرع من فروع شجرة يحمل معه في حركته الأغصان والأوراق (شجرية).
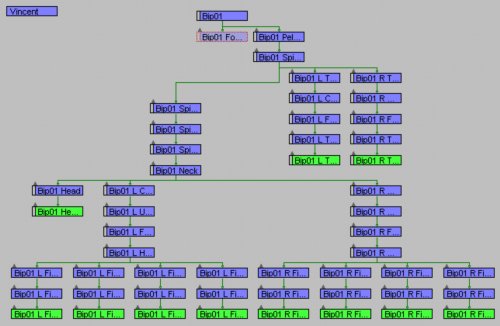
لو أخذنا جسماً كاملاً وحاولنا رسم وترتيب أجزاء الجسم والعلاقات بينها لحصلنا على مخطط متفرع، يمتلك ذلك المخطط جزءاً تلتقي فيه وتبدأ منه العلاقات، يسمى هذا الجزء بجذر البنية الشجرية (root of hierarchy)، تحتاج كل شخصية إلى جذر، ومن المفيد أن يقع ذلك الجذر قريباً من مركز ثقل الشخصية. المخطط الشجري التالي تابع للشخصية فنسنت:
لـوصف العلاقة الحركية بين الأجزاء يتم استخدام تشبيه الأب/الابن (Parent/Child)، حيث الابن يتبع الأب في كل شيء، ولكن الأب لن يتبع الابن، تنطبق هذه العلاقة على الساعد (الأب) واليد (الابن) مثلاً (الشكل 1).
هنالك كذلك العلاقة المسماة بالشقيق (Sibling)، ببساطة عندما يكون لجزئين الأب نفسه، يوصف الجزئان بأنهما شقيقين، ولا شك إن أوضح مثال على ذلك أصابع اليد، حيث إنها جميعاً تمتلك الأب نفسه وهو اليد، لذلك فإن الأصابع بالنسبة لبعضها البعض أشقاء.
كيف يمكن تطبيق وبناء تلك العلاقات برمجياً؟
على سبيل المثال في التشكيل الموجود في الشكل 1، لو أردنا تدوير (rotation) عظمة العضد 45 درجة، يجب علينا تدوير كل العظام التي تقع بعدها بـ 45 درجة أيضاً، كذلك الأمر بالنسبة للانتقال (translation) أو التحجيم (scaling)، في الحقيقة إن ما يجب فعله هو تطبيق جميع تحويلات الأب على أبناءه.
لدمج تأثير الانتقال والتحجيم يمكن استخدام عمليات ضرب المصفوفات أما لدمج تأثير الدوران فيمكن استخدام ضرب المصفوفات أو الرباعيات حيث يمكن استثمار خواص التراكب (composition) والاستيفاء (interpolation) خاصةً عند تطبيق الحركة الديناميكية.
ما هي هذه الـ Quaternion التي أسمع عنها كل هذه الإشاعات؟ما هي هذه الـ Quaternion التي أسمع عنها كل هذه الإشاعات؟
الـ Quaternion يا صديقي هي متجه من أربعة قيم x/y/z/w، تمثل دوران ما في الفضاء، تصف محوراً للدوران وزاوية للدوران حول ذلك المحور بطريقة عجيبة، حيث إنها تُعْتبر متجهاً رباعي الأبعاد (يا للهول!)، وبسبب صفاتها هذه أعتقد إني سأتصرف وأترجمها للعربية إلى "الرباعي"، فائدتها تأتي من العمليات التي يمكن القيام بها ومن أهمها بالنسبة لنا كما ذكرت التراكب (وهو عملية دمج عدة "دورانات" رباعية في متجه رباعي واحد) و الاستيفاء (وهي عملية المزج بين "دورانين" رباعيين بنسبة معينة في متجه رباعي واحد – لاحظ الفرق بين المزج والدمج) إضافة إلى عدد من العمليات الأخرى المفيدة.
وقبل أن أنسى، يمكن تحويل الرباعي من وإلى تمثيل المصفوفة الاعتيادية التي نحبها جميعاً.
تطبيق البنية الشجرية
يستخدم هذا المثال مفهوم البنية الشجرية لعمل ذراع ميكانيكية يمكن التحكم بها عن طريق لوحة المفاتيح، استخدمت ميزة التراكب التي تقدمها المصفوفات لعمل حسابات التحويل ومن ضمنها دمج الدوران، التطبيق يعتمد خط معالجة الرسوميات الثابت (Fixed Function Pipeline) وقد تم حفظ قطع المجسّم له باستخدام نوع ملفات X.
المفهوم الثاني: الحركة العظمية (Skeletal Animation)
يمكن تمثيل أجزاء أي شخصية تمتلك القدرة على الحركة باستخدام مخطط يشبه إلى حد ما الهيكل العظمي المفترض لتلك الشخصية.
تتضمن الحركة العظمية ثلاثة مراحل:
•بناء الهيكل العظمي للشخصية.
•ربط الهيكل العظمي بمجسّم الشخصية وسأتكلم عن ذلك في الجزء التالي.
•تحريك العظام بطريقة متناغمة بحيث توحي إن الكائن يمشي أو يركض مثلاً.
هذه العمليات الثلاث عادةً ما تكون من اختصاص المصممين والمحرّكين، أما المبرمجين فيقتصر عملهم على تطوير طرق لتشغيل والتحكم بالناتج من تلك العمليات في الألعاب أو التطبيقات التي يعملون على تطويرها.
أحد المزايا البرمجية المثيرة للاهتمام الناتجة عن الاعتماد على الهيكل العظمي هي قابلية التحكم بأي من العظام برمجياً، والتي تتيح تنفيذ حركة تتراوح من توجيه رأس الشخصية للنظر نحو شيء ما حتى إمكانية ربط العظام‘ مباشرة بمحرك فيزياء بحيث يمكن عمل حركات فيزيائية ديناميكية مثل السقوط الحر (أو ما يسمى دمية قماشية ragdoll) أو مثلاً ربط سيف أسطوري أو سلاح من أي نوع لعظمة اليد، لا بل يمكنك إعطاء اللاعب القدرة على شراء الدروع المختلفة والتي لكل منها مجسّم مختلف ثم ربط ذلك المجسّم مع عظام الكتف مثلاً، ولقد رأيت كل ذلك بالتأكيد في ألعاب كثيرة متوفرة اليوم.
أود هنا أن أذكر نقطة مهمة بخصوص عملية تحريك الهيكل العظمي، يمكن عمل الحركة للهيكل العظمي يدوياً، ولكن في بعض الأحيان تنتج من عملية تحريك الشخصيات بطريقة يدوية حركة مصطنعة أو غير واقعية، كذلك فإنها تحتاج وقتاً طويلاً إن تم عملها بطريقة متقنة، خاصة في حالة الكائنات العضوية الشبيهة بالبشر لأننا نستطيع تمييز أي خلل في الحركة حتى وإن كان طفيف، لذلك فقد تم تطوير عدة أساليب وطرق تتيح التقاط الحركة (Motion Capture) بحيث ينفذها ممثلين مختصين وتسجّل بواسطة برامج خاصة للحصول على حركة ذات واقعية كبيرة تعتمد على الهياكل العظمية إياها، يتكلم المطوّر همام البهنسي عن الأنواع المختلفة من أنظمة التقاط الحركة في مقالته مقدمة في أنظمة التقاط الحركة [Motion Capture) [BAHNASSI06).
المفهوم الثالث: الجلد (Skin)
لا أعتقد أن الهياكل العظمية تشكّلُ منظراً جميلاً... أليس كذلك؟، نستطيع ربط مجسّم الشخصية بالهيكل العظمي بطريقة بحيث تؤثر حركة كل عظمة على مجموعة من الرؤوس، على سبيل المثال عظمة الساق اليمنى تؤثر على الساق اليمنى من مجسّم الشخصية وكذلك على بعض الأجزاء من منطقة الفخذ الأيمن والقدم بنسب متفاوتة، أي سيتصرف مجسّم الشخصية وكأنه الجلد الذي يتأثر ويتبع العظام في حركته، لتبسيط الفكرة تصور الهيكل العظمي وقد لبس زيّاً تنكرياً، كيف سيتحرك الزي عندما يمشي الهيكل العظمي؟ لذلك يتم وصف الفكرة أحياناً بكلمة "التلبيس".
ولكن كيف يمكن تحقيق كل ذلك عملياً؟
لنأخذ عظمة واحدة،... يتم تعيين قيمة لكل رأس مثلث تؤثر عليه العظمة المأخوذة تتراوح هذه القيمة من 0.0 إلى 1.0 حيث 0.0 تعني إن حركة العظمة لن تؤثر إطلاقاً على الرأس، بينما القيمة 1.0 فتعني إن الرأس سيتبع العظمة في حركتها بالكامل، تسمى هذه القيمة وزن الرأس (vertex weight) أو وزن المزج (blend weight) ويتم تعيينها في معظم الأحيان عن طريق برامج التصميم ثلاثي الأبعاد التي تقدم أدوات مساعدة مختصة، لاحظ أنه من الممكن لأي عدد من العظام التأثير على رأس واحد كل منها تؤثر عليه بوزن معين (أو نسبة معينة إن شئت)، ولكن لأسباب عملية من الأفضل وضع حد أقصى لعدد العظام التي تؤثر على كل رأس عادة ما يكون ذلك الحد 3 أو 4 عظام لكل رأس في التطبيقات الفورية.
يطلق على عملية ربط الهيكل العظمي بالمجسّمات وتحديد الأوزان لكل العظام بالتلبيس skinning وهي عملية يجب أن يقوم المصمم بها بدقة متناهية لأن الأوزان إن لم تكن دقيقة ستحصل تشوهات أثناء الحركة (كما ستلاحظ في حركة الشخصية فنسنت الذي لم أقم بعملية تحديد الأوزان له جيداً بسبب قلة الخبرة في هذا المجال).
من الناحية البرمجية، عند تحميل الشخصية، يجب على البرنامج القيام بعملية حساب التحويل (transformation) لكل رأس في المجسّم عن طريق معادلة تأخذ في الحسبان العظام التي تؤثر على الرأس ومقدار تأثير كل منها، يمكن القيام بالعملية برمجياً (أي باستخدام المعالج المركزي) أو يمكن كتابة مظلل رؤوس vertex shader يحسب التحويل على المعالج الرسومي (وهي الطريقة الأفضل في معظم الأحيان). كذلك يجب حساب التحويل لكل ناظم (normal) للحصول على إضاءة صحيحة، بنفس الطريقة التي حُسِب التحويل للرأس بها، ولكن يجب استخدام مقلوب معكوس مصفوفات التحويل للعظام (inverse transpose of matrix)، عندما يقتصر التحويل في المصفوفة على الانتقال (translation) والدوران (rotation) فقط، شاءت الأقدار أن يكون معاكس المصفوفة هو المصفوفة الأصلية نفسها! لذلك فلا حاجة لحساب المعاكس لمصفوفة عظام لم يتم تحجيمها (scaled) أو إسقاطها (projected).
المعادلة العامة لحساب الموضع النهائي للرأس حسب عدد الأوزان [CHANNA01]
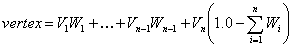
حيث:
- vertex: الرأس النهائي
- Vn: الرأس رقم n
- Wn: وزن الرأس رقم n
بحيث تصبح المعادلات في حالة اثنين، ثلاثة، وأربعة رؤوس كالتالي:
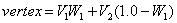
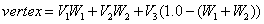
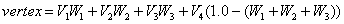
مثال: الإجراء التالي يقوم بحساب مواقع الرؤوس باستخدام أوزانها مع مراعاة إعادة حساب ناظم الرؤوس للحصول على إضاءة صحيحة:
struct VertexB4
{
D3DVECTOR Position; // موقع الرأس
D3DVECTOR Normal; // الناظم على الرأس
FLOAT fWeights[4]; // الأوزان الأربعة للرأس
BYTE btIndices[4]; // العظام الأربعة التي تؤثر على الرأس
DWORD Diffuse; // اللون الإنتشاري
FLOAT tu, tv; // إحداثيات الإكساء
}
void BlendVertexNew(D3DVECTOR* result,D3DVECTOR* normal,
ChararacterVertex* vec0, D3DMATRIX* mat0, D3DMATRIX* mat1)
{
D3DVECTOR locVec0, locVec1;
D3DMATRIX norMat0 = *mat0,norMat1 = *mat1;
MulVecMat(&locVec0, &vec0->vertex, mat0);
MulVecMat(&locVec1, &vec0->vertex, mat1);
//إحسب موقع الرأس الجديد حسب الوزن
result->x = (vec0->fWeight * locVec0.x) + ((1.0f - vec0->
fWeight)*(locVec1.x));
result->y = (vec0->fWeight * locVec0.y) + ((1.0f - vec0->
fWeight)*(locVec1.y));
result->z = (vec0->fWeight * locVec0.z) + ((1.0f - vec0->
fWeight)*(locVec1.z));
MAKETRANSMAT(norMat0,0,0,0) ; //لا إزاحة
MAKETRANSMAT(norMat1,0,0,0) ; //لا إزاحة
result->x = (vec0->fWeight * locVec0.x) + ((1.0f - vec0->
MulVecMat(&locVec0,&vec0->normal,&norMat0) ;
MulVecMat(&locVec1,&vec0->normal,&norMat1) ;
// إحسب الناظم الجديد للرأس
// بافتراض عدم وجود تحجيم، فقط انتقال ودوران
normal->x = (vec0->fWeight * locVec0.x) + ((1.0f - vec0->
fWeight)*(locVec1.x)) ;
normal->y = (vec0->fWeight * locVec0.y) + ((1.0f - vec0->
fWeight)*(locVec1.y)) ;
normal->z = (vec0->fWeight * locVec0.z) + ((1.0f - vec0->
fWeight)*(locVec1.z)) ;
}
مثال: مظلل الرؤوس التالي المكتوب بلغة Cg يقوم بالعملية نفسها، ولكن باستخدام طريقة مختلفة قليلاً، حيث أنه يجمع تأثير كل مصفوفة على الـ vertex ليحصل على الموقع النهائي، كذلك فإنه يحتسب الإضاءة لضوء واحد.
ستلاحظ استخدام 72 متغير من نوع float4 لتمثل 24 مصفوفة تحويل كل منها 3x4، يفترض هذا المظلل أن شخصيتك بكاملها تمتلك ما يصل إلى 24 عظمة، يجب أن تمرر القيم لـ matrixIndex مضروبة بـ 3 لكي تحصل على المصفوفة الصحيحة (أي يجب حساب ذلك في التطبيق نفسه)، يمكن كذلك استخدام 24 مصفوفة كل واحدة من نوع float3x4، ولكن تم كتابة هذا المظلل بهذه الطريقة للحصول على أداء أفضل. [NVIDIA03]
void cg_skin4m( float3 position : POSITION,
float3 normal : NORMAL,
float2 texCoord : TEXCOORD0,
float4 weight : TEXCOORD1,
float4 matrixIndex : TEXCOORD2,
out float4 oPosition : POSITION,
out float2 oTexCoord : TEXCOORD0,
out float4 color : COLOR,
uniform Light light,
uniform float4 boneMatrix[72], // 24 matrices each 3x4
uniform float4x4 modelViewProj )
{
float3 netPosition = 0, netNormal = 0;
for (int i = 0; i < 4; i++)
{
float index = matrixIndex[i];
// بافتراض عدم وجود تحجيم، فقط انتقال ودوران لن نحتاج معكوس المصفوفة
float3x4 model = float3x4(boneMatrix[index + 0],
boneMatrix[index + 1],
boneMatrix[index + 2]);
float3 bonePosition = mul(model, float4(position, 1));
float3x3 rotate = float3x3(model[0].xyz,
model[1].xyz,
model[2].xyz);
float3 boneNormal = mul(rotate, normal);
netPosition += weight[i] * bonePosition;
netNormal += weight[i] * boneNormal;
}
netNormal = normalize(netNormal);
oPosition = mul(modelViewProj, float4(netPosition, 1));
oTexCoord = texCoord;
color = computeLighting(light, netPosition, netNormal);
}
لم أضع هنا تعريف إجراء computeLighting ولا الهيكل Light للاختصار، ستجد المظلل الكامل في الملفات المرفقة مع المقالة.
إحدى المزايا المهمة للحركة الهيكلية العظمية باستخدام الجلد هي إن عدة شخصيات متشابهة يمكنها مشاركة الهيكل العظمي والحركة نفسها، مثلاً لو كانت لعبتك تحتوي على 100 شخصية مختلفة الشكل، نصفهم من مصاصي الدماء والنصف الآخر من المستذئبين، يمكنك استخدام هيكلين عظميين فقط للكل، أحدهما لمصّاصي الدماء والآخر للمستذئبين، ويمكنك كذلك مشاركة الحركة نفسها بين جميع مصاصي الدماء وبين جميع المستذئبين، لتحصل في النهاية على معركة لم يسبق لها مثيل!

تطبيق الجلد: يستخدم هذا المثال مفهوم الحركة الهيكلية العظمية باستخدام الجلد، عن طريق عمل ذراع بشكل متوازي مستطيلات ثم التأثير عليه بواسطة عظمتين أوزانهما متدرجة على امتداد الذراع، يمثل ذلك أبسط مثال ممكن حول هذا النوع من الحركة، يتم بناء مجسّم الذراع حسابياً (أي أثناء التنفيذ) ويمكنك تغيير خصائص الذراع عن طريق تغيير الثوابت الموجودة في بداية ملف winmain.cpp.
يستخدم هذا المثال مظلل رؤوس مكتوب باستخدام HLSL لتحقيق الهدف، وهو يعتمد على معادلات الأوزان التي استعرضناها قبل قليل، الشفرة المصدرية للمظلل (skin_shader.fx) تحوي تعليقات مفصلة حول كل خطوة. يقوم المظلل أيضاً بحساب الإضاءة لكل رأس لضوء اتجاهي واحد، الإضاءة الناتجة من النوع الانتشاري فقط Diffuse. بسبب استخدام مظلل فإن هذا المثال يحتاج بطاقة شاشة تدعم على الأقل مظللات الرؤوس من الإصدار 1.1.
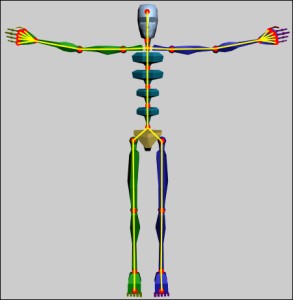
المفهوم الرابع: الوضعية الابتدائية (Initial Pose)
انظر للشكل 3، هل تلاحظ كيفية مد الذراعين على الجوانب بطريقة ملفتة للنظر وكيف أن الوقفة بكاملها منتظمة للغاية؟ لا شك أنك قد رأيت الوضع نفسه في أماكن أخرى، في مجال حركة الشخصيات يسمى هذا الوضع بالوضعية الابتدائية (Initial Pose) أو الوضعية القياسي (Default Pose) ويمكنك اعتبارها نقطة البداية لحركة الشخصية، يتم مد الذراعين لكي تحصل على أفضل نتائج ممكنة عند تحريكهما وثنيهما، في الحقيقة يتم بناء مجسّم الشخصية منذ البداية لتتخذ الوضع إياه ثم يتم تعديل الهيكل العظمي بحيث يتخذ الوضع نفسه بعد ذلك يتم ربطه بمجسّم الشخصية.
بالنسبة للمبرمج، فإن هذا الوضع هو شكل الهيكل العظمي الأصلي قبل تحريك أي من العظام، إي بدون أي تحويلات، وفائدته أنه يستخدم كنقطة البداية والمرجع لتطبيق التحويلات الحركية على العظام.
حتى الآن لم نستخدم فنسنت في أي شيء ولكن الآن سأطلب منه توضيح فكرة الوضع الأساسي (لا تسألني ما سبب امتلاكه لـ 4 أصابع فقط، الحوادث تقع كما تعلم...):

المفهوم الخامس: مفاتيح الحركة (Animation Keyframes)
لا شك أن الجميع يعلم أنّ الحركة والزمن مرتبطان بشكل كبير، ولكل حركة عدد أطر محدّد في الثانية الواحدة، على سبيل المثال لو افترضنا أن نظام الحركة قد تم ضبطه بحيث أن أقصى عدد من الأطر في الثانية هو 10، وفرضنا كذلك أنه لدينا حركة تستغرق 30 ثانية، فذلك يعني أن الشخصية تحتاج 300 إطار حركة أي في واقع الأمر 300 وضع للهيكل العظمي! أي لو كان الهيكل العظمي يمتلك 30 عظمة فسنحتاج لحفظ 9000 تحويل حركي، تلك أعداد كبيرة بالتأكيد كما أنها تتطلب جهداً كبيراً ووقتاً طويلاً إن تم عمل كل واحدة من الأوضاع يدوياً.
لذلك فقد تم استنباط فكرة مفاتيح الحركة، الفكرة من ورائها هي أنك لن تحتاج في معظم الحالات إلى تحديد الوضع لكل إطار، يمكنك فقط عمل الأوضاع الرئيسية من الحركة (وهي ما يسمى مفاتيح الحركة) وترك التطبيق الذي يقوم بتشغيل الحركة يملئ الفراغ بين المفتاح السابق واللاحق عن طريق عمل استيفاء (interpolation) بين التحويلات السابقة والتحويلات اللاحقة، انظر الشكل 4 مثلاً، ليس من الضرورة أيضاً إضافة تحويلات للعظام التي لن تتحرك، فقط تلك التي تتحرك، باستخدام هذه الفكرة تم اختصار التحويلات الحركية مما يعني التقليل من كمية البيانات التي يجب حفظها ومعالجتها وتسهيل عملية التحريك.

ولكن يجب عمل الاستيفاء (interpolation) من ضمن التطبيق، وذلك هو العيب الوحيد تقريباً لهذه الفكرة، وهو أن الكلفة الحسابية ترتفع بمقدار معين، ولكن بما أن حركة العظام تقتصر على الدوران فقط في معظم الأحيان فمن الأفضل استخدام الرباعيات والتي تقدم عملية استيفاء للدوران تستخدم ما يسمى الاستيفاء الخطّي الكروي (Spherical Linear Interpolation) والذي عادة ما يختصر Slerp.
ماذا؟ لديك نفس سؤال؟ هل يمكن عمل الموضوع باستخدام المصفوفات؟
أجل طبعاً! ولكن ستصبح العملية أصعب وأطول وأكثر كلفة حسابياً و.. من الأفضل الابتعاد عن المتاعب كما تعلم، بالنسبة لعمليات الدوران والاستيفاء باستخدام مفاتيح الحركة فإن الرباعيات هي العصا السحرية.
المفهوم السادس: مزج الحركة (Animation Blending)
هل من الجنون المزج بين مجموعتين من مفاتيح الحركة تمثلان حركتين مختلفتين بنسب معينة؟ كلا طبعاً، ولهذه الميزة فوائد رائعة، على سبيل المثال لو كانت لدينا حركة مشي وحركة ركض، يمكنك باستخدام عملية مزج الحركة جعل الانتقال بين المشي والركض سلس وواقعي جداً عن طريق مزج الحركتين بنسب متفاوتة مع بعض، فمثلاً تستطيع الشخصية أن تمشي بسرعة عن طريق إضافة القليل من حركة الركض على حركة المشي (لنقل 20% ركض و80% مشي) ماذا يحصل لو طبقنا نفس النسب بالعكس؟ ستبدأ الشخصية بالهرولة!
فائدة أخرى هي إمكانية استخدام حركة خاصة لأجزاء معينة من جسم الشخصية مع عدم التأثير على باقي الجسم، يمكن هكذا مثلاً جعل الشخصية تلوّح باليد أثناء مشيها عن طريق تطبيق حركة المشي على حدة (والتي تشمل الجسم بأكمله) ثم حركة اليد التي تلوّح على حده (والتي تؤثر على اليد فقط)، ثم دمج الاثنين معاً.
المفهوم السابع: حركة الوجه (Facial Animation)
إحدى أنواع الحركات الأصعب تطبيقاً بشكل صحيح هي حركة الوجه، لأن الكثير يحصل في الوجه، مثلاً يمكنك أن تعرف إن الشخصية حزينة، سعيدة، مليئة بالعزم، يائسة، غاضبة، خائفة وكل ذلك من تعابير الوجه فقط، إضافة إلى حركة الشفاه عند الكلام وحركة العيون. يمكن تطبيق حركة الوجه عملياً باستخدام إحدى طريقتين لكل منهما مزايا وعيوب:
أولاً: طريقة العظام
كما استخدمنا العظام لتحريك الجلد بنسب مختلفة، يمكن إضافة عدد من العظام للوجه كل منها يتحكم بجزء ما، على سبيل المثال أحد العظام يتحكم بالفك الأسفل، عندها يمكن تحريك الفك الأسفل مباشرة للحصول على تأثير الكلام مثلاً.
ميزة هذه الطريقة هي امتداد لمزايا الهيكل العظمي والجلد، حركات الوجه قابلة للتحكم برمجياً بشكل مباشر، وكذلك يمكن تطبيق الحركات نفسها على أي عدد من الشخصيات بشكل مباشر (بشرط إن جميعها تستخدم هيكل عظمي مشابه)، إضافة إلى إنها لا تحتاج الكثير من مساحة الذاكرة عند الاستخدام. أما عيوبها فهي أن عدد العظام التي تحتاجها للحصول على حركة وجه يمكن وصفها بالواقعية كبير جداً، بالعشرات، من ما يجعل تحريك الوجه يدوياً أو برمجياً مهمة صعبة، كذلك هنالك بعض التعبيرات التي لا يمكن تطبيقها بشكل مباشر باستخدام هذه الطريقة، مثل تقطيب الجبين.
ثانياً: طريقة الحركة التحوّلية (Morphing)
وتسمى أيضاً (Tweening) في هذه الطريقة يقوم فنان تصميم الشخصيات ثلاثية الأبعاد بعمل مجسّم وجه لكل تعبير مطلوب للشخصية على حدة، أي كل تعبير هو مجسّم منفصل، يجب أن تكون جميعها نسخ معدلة من مجسّم الوجه الأصلي نفسه.
للحصول على الحركة يتم تطبيق معادلة مزج بين تعبيرين أو أكثر بنسب معينة بالتدرج للحصول على تحوّل ناعم، تصور إن لديك مجسّمين أحدهما لكرة والآخر لصندوق والاثنان يمتلكان نفس عدد الوجوه والرؤوس تماماً، تطبيق الحركة التحولية بينهما يعطيك مجسّم يتحول من كرة إلى صندوق (أو العكس) بمرور الزمن، هذه الطريقة استخدمت في الماضي لتحريك الشخصيات نفسها بالكامل بدل استخدام العظام، على سبيل المثال لعبة Quake الأولى من شركة Id استخدمت الحركة التحوّلية لعمل حركة الشخصيات فيها، في الحقيقة إن نوع ملفات md2 يستند على هذا المفهوم.
بالعودة لحركة الوجوه، تعطي هذه الطريقة حرية كبيرة للفنانين ونتائج مرئية رائعة، ولكن مشكلتها هي إن التعابير يجب عملها يدوياً من قبل الفنان لكل شخصية في اللعبة، وبما إن كل تعبير سيكون في مجسّم منفصل فذلك يعني مساحة كبيرة من الذاكرة. ولكن مع ذلك وبسبب النتائج الدقيقة التي يمكن الحصول عليها عند استخدام الحركة التحوّلية فإن هذه الطريقة مستخدمة بكثرة حالياً ليس فقط في الألعاب ولكن في مجال الأفلام أيضاً، على سبيل المثال، في الشكل 5 يظهر تعبيرين من الصعب تمثيلهما لو تم استخدام الطريقة الأخرى.

أما لتطبيق هذا المفهوم عملياً فإن المعادلات التي يمكنك استخدامها شبيهة تماماً بالمعادلات التي تستخدم لحساب تأثير عظمتين أو أكثر على رأس والتي تكلمنا عنها بتفصيل كافي في المفهوم الثالث (الجلد)، ولكن أبسط من ذلك حيث بدل استخدام الأوزان نستخدم نسبة للتحوّل، وبالطبع يمكن المزج بين أكثر من تعبيرين.
تطبيق الحركة التحوّلية: يستخدم هذا المثال مفهوم الحركة التحوّلية لتحريك وجه باستخدام عدة تعبيرات، يتم تنفيذ الحركة باستخدام مظلل رؤوس (morphing_shader.fx) يستخدم معادلات المزج المذكورة للتحويل بين تعبيرين، أقصى عدد من التعبيرات التي يمكن تحميلها في الوقت الواحد هو 6، كذلك فإن المظلل يقوم بإضاءة الرؤوس بطريقة بسيطة باستخدام ضوء اتجاهي واحد. المجسّم المستخدم كمثال تم تصديره من 3D Studio MAX إلى هيئة خاصة بسيطة جداً باستخدام مصدّر صغير مكتوب باستخدام MaxScript، تجد ملف المصدّر في المجلد maxexporter. لأن هذا المثال يستخدم مظلل رؤوس، فإنه يحتاج بطاقة عرض تدعم على الأقل مظللات الرؤوس من الإصدار 1.1. هل يمكن تصور Batman وهو يطير ويقاتل من دون عباءته؟ و يا لها من خيبة أمل عندما يكون العلم المرفوع لا يرفرف مع الريح، ماذا لو أردت جعل شعر أحد الشخصيات يتحرك مع الريح بطريقة واقعية؟ للحصول على تأثيرات واقعية من هذا النوع يجب عمل محاكاة للأجسام المرنة أو ما يسمى محاكاة الملابس، أساس هذه المحاكاة يعتمد فيزياء النوابض (Spring Physics).
المفهوم الثامن:محاكاة الملابس (Cloth Simulation)
هل يمكن تصور Batman وهو يطير ويقاتل من دون عباءته؟ و يا لها من خيبة أمل عندما يكون العلم المرفوع لا يرفرف مع الريح، ماذا لو أردت جعل شعر أحد الشخصيات يتحرك مع الريح بطريقة واقعية؟ للحصول على تأثيرات واقعية من هذا النوع يجب عمل محاكاة للأجسام المرنة أو ما يسمى محاكاة الملابس، أساس هذه المحاكاة يعتمد فيزياء النوابض (Spring Physics).
تستند فيزياء النوابض على خصائص المرونة (Elasticity) والتي تعني أن الجسم رغم مرونته يميل إلى العودة إلى شكله الأصلي عند توقف القوى الخارجية عن التأثير عليه، وكذلك فإنها تعتمد تأثير عاملي الضغط (strain) والشد (stress) على مكوّنات الجسم المرن.
يتم تمثيل الجسم المرن عادة بشكل مجموعة نقاط تسمى نقاط الكتلة تربط بينها نوابض (انظر الشكل 6)، قد تشكل مجموعة النقاط شكلاً أحادي البعد (مثل الحبل) أو ثنائي البعد (مثل الملابس أو سطح الماء) أو حتى ثلاثي البعد (مثلاً الكرات المرنة Blobs)، يعتمد التعقيد الحسابي للنظام الناتج على عدد نقاط الكتلة وكيفية ارتباطها ببعضها البعض.
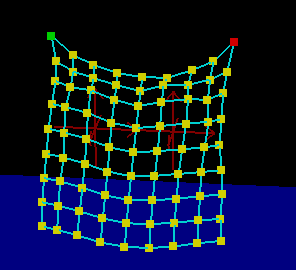
معظم الألعاب الموجودة حالياً تستخدم هذا المفهوم، والنتائج المرئية تستحق التعب، لن أتعمق أكثر في الموضوع لأنه يقع خارج نطاق هذه المقالة، ولكن أتمنى أن أكون قد أثرت اهتمامك حوله.
المفهوم التاسع: الحركية الأمامية (Forward Kinematics) والحركية العكسية (Inverse Kinematics)
كما قلنا في ما سبق، حركة الشخصيات باستخدام الهيكل العظمي والجلد تعطي إمكانية التحكم مباشرة بأي جزء من الشخصية، لنأخذ هذا الموضوع خطوة للأمام، لنفترض أن شخصيتك تقف الآن أمام باب وتود فتحه عن طريق مقبض الباب، كيف تحصل على حركة صحيحة لهذه العملية بحيث تمد الشخصية يدها وتمسك المقبض ثم تديره وتدفع الباب؟
قد تقول إنك ستقوم بعمل حركة اليد وهي تفتح الباب في برنامج التصميم ثم مزجها مع حركة الوقوف للشخصية أثناء التنفيذ، وهذه الفكرة صحيحة، ولكن ماذا لو كان هنالك عدة أنواع من الأبواب كل منها تحتوي على مقبض مختلف في مكان مختلف؟ لديك حركات كثيرة للأيدي لتعملها، ولتصبح الأمور أسوأ ماذا لو أردت أن تقوم الشخصية بالتقاط شيء ما من الأرض أو من على طاولة؟ يمكنك بالطبع الالتفاف على الفكرة واستخدام حركة بسيطة غير دقيقة لتبسيط الأمور (كما تفعل الكثير من الألعاب)، ولكن هنالك طرق رياضية لاحتساب هذا النوع من الحركات بشكل صحيح، وقد تم استخدامها فعلاً في بعض الألعاب لتضفي صفة الواقعية الفيزيائية للحركة.
الطريقة الرياضية الأولى تسمى الحركية الأمامية (Forward Kinematics)، لنفترض إن لديك ذراع متموضعة بطريقة معينة (أي لكل مفصل زاوية معينة) وتمتلك هذه الذراع مفصل أول ثابت (قاعدة الذراع مثلاً أو عظمة الكتف في حالة الشخصيات)، الحركية الأمامية تُستخدم لحساب الموقع النهائي لأي جزء من الذراع من زوايا المفاصل التي سبقته بدءاً بأول مفصل حتى تصل إلى الجزء المطلوب، وقد استخدمنا طريقة مشابهة لذلك فعلاً! حيث إن الحركة الهيكلية العظمية تستند على هذا المفهوم.
الطريقة الثانية تسمى الحركية العكسية (Inverse Kinematics) وهي عكس الأولى كما استنتجت بلا شك ، لو كنا نمتلك ذراعاً متحركة، على سبيل المثال ذراع الشخصية نفسها، وكنا نرغب أن تصل الذراع إلى كرة موضوعة على طاولة مثلاً بافتراض إن المسافة بين الذراع والكرة مناسبة، فإن الحركية العكسية تبدأ من عظمة اليد وتستمر بالتدريج صعوداً لتحتسب الزاوية المطلوبة لكل جزء من الذراع بحيث تصبح الذراع لا بل الجسم بأكمله في الوضع الصحيح لإمساك الكرة الحركية العكسية هي أداة قوية وهنالك تطبيقات ضخمة عليها، تستخدم مثلاً في عالم الروبوتات، يمكنك الذهاب لحدود أبعد كثيراً من مجرد التقاط كرة، على سبيل المثال جعل حركة الشخصية بأكملها ديناميكية، أي إن الشخصية تمشي وتركض وتصعد وتنزل وتقفز بواسطة حسابات فيزيائية بدل استخدام حركة مخزونة مسبقاً، ولكن بالطبع تلك الحسابات عادة ما تكون معقدة جداً لدرجة أن بعضها غير مناسب للتطبيقات الفورية، ولكن كما في كل شيء هنالك طرق للالتفاف حول التعقيد، على سبيل المثال شركة Natural Motionتقدم أنظمة متكاملة لحركة الشخصيات الديناميكية مستخدمة في عدد من الألعاب التجارية الحديثة وبمجرد مشاهدة إحدى مقاطع الفيديو التي يقدموها ستكتشف بنفسك الفرق بين الحركة الاعتيادية والحركة الديناميكية، فرق شاسع! ستجد إحدى مقاطع الفيديو في الملفات المرفقة مع هذه المقالة.
يتبع - الجزء الثاني: استخدام مكتبة Cal3D لتحريك الشخصيات
لمزيد من المعلومات