يتعرف مبرمج الرسوميات على العديد من المصطلحات الجديدة في بادئ مسيرته. ليست كلها بسيطة أو واضحة، فمنها ما يفهمه ويستوعبه، ومنها يمرّ عليه ويتجاهل فهمه، فقط لأن هذه المصطلحات تبدو أكثر غموضاً. لا يهم… لكني أحب حقاً من آن لآخر أن أتساءل (من السؤال، وليس السآلة… مع أني أفعل الثانية كثيراً) عن أصل شيء ما أصبحنا نستخدمه ونفترض وجوده بالبديهة. مثلاً، لماذا نستعمل الإكساءات؟ ألا توجد طريقة أخرى أفضل لتحقيق نفس الهدف؟ وهكذا…
اليوم سأطرح موضوعاً من هذا القبيل، لكنه ليس عن إكساء، وإنما عن ناظم… من ناظم؟… ليس ناظم الغزالي طبعاً، فالرجل ينعم في قبره الآن لا يعيش الجنون الحاصل في بلده العراق هذه الأيام… نحن نتحدث عن ناظم آخر…
يقولون أن المجسمات تتألف من سطوح، كل سطح هو مضلع بسيط، ولنقل المثلث، وهذا المثلث يتألف من رؤوس ثلاثة… كل رأس يحمل معلومات معينة… هي إحداثيات موقعه في الفراغ، والناظم، وربما إحداثيات إكساء، وربما لون.
struct VERTEX // بنية رأس مجسم
{
float posX, posY, posZ; // إحداثيات الموقع الفراغية
float normalX, normalY, normalZ; // الناظم
float texU, texV; // إحداثيات الإكساء
};
لحظة لحظة… الموقع في الفراغ مفهوم… واللون مفهوم (لو أردنا أن نلون المجسم مثلاً بألوان مختلفة)، لكن من هذا الناظم؟ وما هي إحداثيات الإكساء؟
دعنا الآن من إحداثيات الإكساء، فهي ليست محط اهتمامنا اليوم… ولنعد إلى ناظم. الناظم يا سيدي الكريم، هو متجه ينطلق من السطح وباتجاه عمودي على السطح. انظر الصورة أدناه مثلاً:
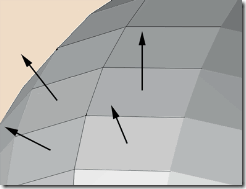
لاحظ في الصورة أن النواظم تنطلق من منتصف السطح. في الحقيقة طالما أننا نتحدث عن سطح مستوٍ، فالناظم سيكون نفسه مهما تغيرت نقطة انطلاقه. أما للأسطح المنحنية، فالناظم دائماً عمودي على المنحني، كما في الصورة هذه:
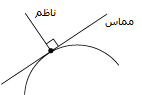
إذن الناظم هو العمود على السطح (أو العمود على مماس السطح) في نقطة منه. لكن لدينا مشكلة هنا، المجسمات الفراغية في رسوم الحاسوب تتألف من عدد من المضلعات المسطحة، والتي تتكاثف عندما نريد تمثيل السطوح المنحنية بها. بعبارة أخرى، الشكل الأصلي هو منحني، لكننا -ولقيود ما- نضطر لبنائه من مضلعات. لذلك فإن النواظم يجب أن تمثل الشكل المنحني قدر الإمكان وليس الشكل المضلع.. لهذا، نجد أن رؤوس المضلعات في المجسمات في رسوم الحاسوب تحمل معها قيمة الناظم، فالناظم عند الرأس قادر على التعبير عن انسيابية الشكل الأصلي كما في الصورة أدناه:
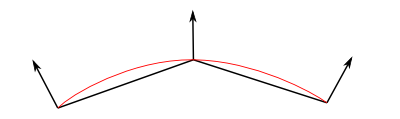
تعال معي الآن لننظر إلى بعض تبعات هذا الكلام…
تستخدم النواظم في رسوميات الحاسوب لحساب إضاءة السطوح. فكلما قابل اتجاه الناظم اتجاه الضوء ازداد سطوع السطح. في الصورة أدناه المتجه ن هو الناظم الخارج من السطح، والمتجه ل هو اتجاه الضوء القادم على السطح. الزاوية بينهما وقدر رمزنا لها بالحرف ز هي ما يحدد مقدار السطوع. عندما تصغر الزاوية ز يسطع السطح أكثر بسبب مقابلته للضوء.
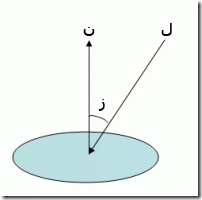
تأمل في الصورة التالية الآن وحاول تبرير الفرق بين الكرتين أدناه وفقاً لما قرأته للتو:

نعم بالضبط، الكرة اليمنى استخدمت نواظم عمودية على أسطح المضلعات المكونة للكرة، بينما اليسرى استخدمت نواظم "ناعمة" تعبر عن المنحني الأصلي لشكل الكرة. الفرق واضح جداً 
فقط للعلم، في رسوم الحاسوب، يسمى أسلوب تظليل الكرة اليمنى بأسلوب التظليل المسطح (faceted shading)، أما الكرة اليسرى فمظللة بأسلوب جوروه (Gauraud shading). حيث أن نظرية الأخ جوروه (وهو عالم رسوميات معاصر، وليس أحد زعماء لعبة مورتال كومبات رباعيو الأذرع إياهم) أننا نستطيع الحصول على تظليل ناعم لو كانت نواظم السطوح المشكلة للمجسم ناعمة…
يمكننا الدخول بالتفاصيل الرياضية للنواظم واشتقاقها من الأشكال الأصلية، لكنني لا أريد إطالة التدوينة أكثر من هذا… لذا أرجو بهذا أن تكون أيها القارئ العزيز قد عرفت السبب الأصلي وراء تحديد النواظم على رؤوس المجسمات في رسوم الحاسوب… ونتابع حديثنا في تأملات رسومية أخرى 